Lab 7: Kalman Filter

1. Objective

The main goal of lab7 is to implement a Kalman Filter which can help me to supplement the slowly sampled ToF values. After that, it can help the robot to run torwards the wall in a faster speed and stop at 1 feet.

2. Lab tasks

2.1 Estimate drag and momentum

The step response I choose is 150. The maximum PWM value is 255 and this value is suitable for estimating the drag and momentum. This value can help the robot to test the steady state.

From the graph below, it can be observed that the steady state speed is about 2000 mm/s. The 90% rise time is 1.13s.

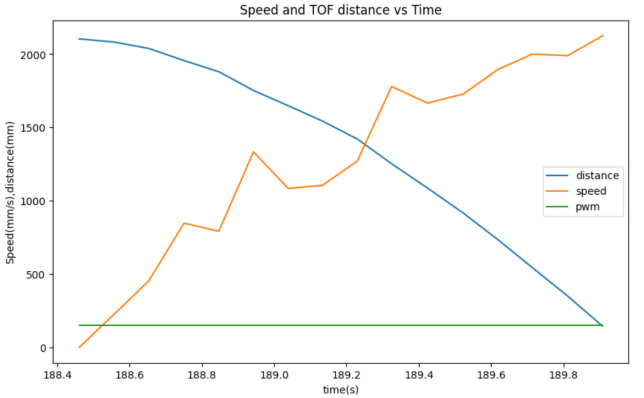
Therefore:

$ d = \frac{u}{x'} = \frac{150}{2000} = 0.075$

$ m = \frac{-dt_{0.9}}{ln(1-0.9)} = \frac{-0.075*1.13}{ln(0.1)} = 0.037$

Therefore, the A matrix and B matrix are:

$$ \begin{bmatrix} 0 & 1 \\ 0 & \frac{-d}{m}=-2.03 \\ \end{bmatrix} $$

$$ \begin{bmatrix} 0\\ \frac{1}{m}=27.03\\ \end{bmatrix} $$

$$ \begin{bmatrix} -1 & 0\\ \end{bmatrix} $$

2.2 Initialize KF (Python)

First, we need to initialize Ad and Bd following the equation:

$ Ad = (I+dt*A)$

$ Bd = dt*B)$

The sample period dt I choose is about 0.2s. Following the instructions from class the Σu and Σz are:

$$ \begin{bmatrix} σx^{2} & 0 \\ 0 & σv^{2} \\ \end{bmatrix} $$ $$ \begin{bmatrix} σz^{2}\\ \end{bmatrix} $$

Here the σz=20 and σx=σv=

$ \sqrt{10^{2}*\frac{1}{dt}} $

2.3 Implement and test your Kalman Filter in Jupyter (Python)

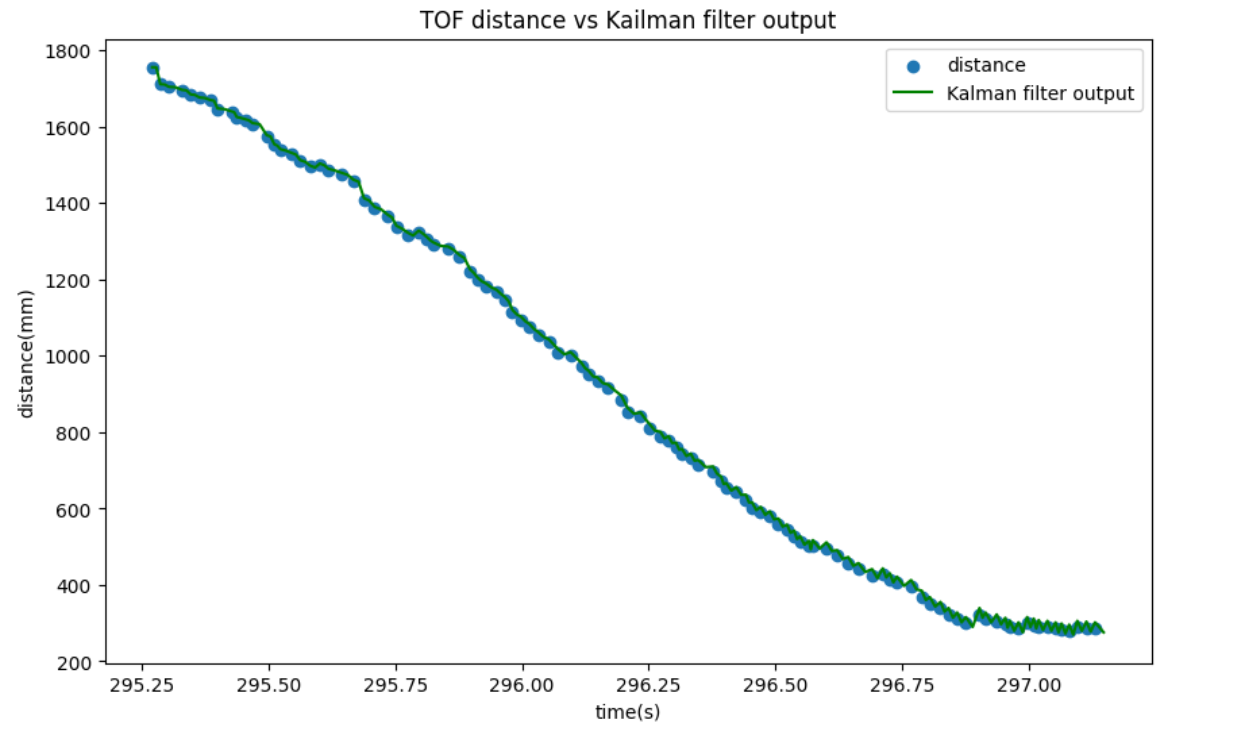
Following the instruction and the code, I get the output of Kalman filter. In order to get a more accurate output, I decrease σz to 5. Here is the code and the result of estimated distance and the real distance.


        kf_out=[]
        kf_vel=[]
        sigma = sig_u
        u = np.array([[-1756],[0]])
        for t,mo,d in zip(time_array,pwm_array,dist_array):
            mu,sigma = kf(u,sigma,mo/150,d)
            kf_out.append(mu[0][0])
            kf_vel.append(mu[1][0])

Although the estimated distance is correct, the estimated speed is inaccurate and I can not figure out the reason.

2.4 (5000) Faster frequency

If I use the Kalman filter in a faster speed, I need to use only the prediction step to estimate the state. The new Kalman filter in python should be:


            def kf_pred(mu,sigma,u,y,update):

                mu_p = A.dot(mu) + B.dot(u)
                sigma_p = A.dot(sigma.dot(A.transpose())) + sig_u

                if(update):
                    sigma_m = C.dot(sigma_p.dot(C.transpose())) + sig_z
                    kkf_gain = sigma_p.dot(C.transpose().dot(np.linalg.inv(sigma_m)))

                    y_m = y-C.dot(mu_p)
                    mu = mu_p + kkf_gain.dot(y_m)
                    sigma=(np.eye(2)-kkf_gain.dot(C)).dot(sigma_p)
                else:
                    mu=mu_p
                    sigma=sigma_p
                return mu,sigma

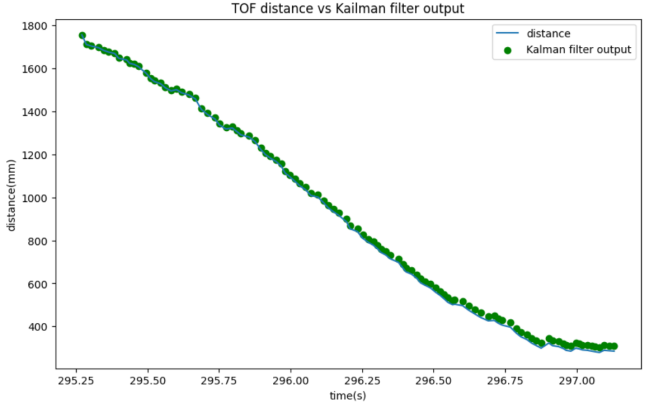
The frequency of kalman filter is twice the frequency of ToF readings. The result is shown below.

Back to the main page